47 Principles for Creating Categories
“The What and Why of Categories” explained what categories are and the contrasting cultural, individual, and institutional contexts and purposes for which categories are created. In doing so, a number of different principles for creating categories were mentioned, mostly in passing.
We now take a systematic look at principles for creating categories, including enumeration, single properties, multiple properties and hierarchy, probabilistic, similarity, and theory- and goal-based categorization. These ways of creating categories differ in the information and mechanisms they use to determine category membership.
Enumeration
The simplest principle for creating a category is enumeration; any resource in a finite or countable set can be deemed a category member by that fact alone. This principle is also known as extensional definition, and the members of the set are called the extension. Many institutional categories are defined by enumeration as a set of possible or legal values, like the 50 United States or the ISO currency codes (ISO 4217).
Enumerative categories enable membership to be unambiguously determined because a value like a state name or currency code is either a member of the category or it is not. However, this clarity has a downside; it makes it hard to argue that something not explicitly mentioned in an enumeration should be considered a member of the category, which can make laws or regulations inflexible. Moreover, there comes a size when enumerative definition is impractical or inefficient, and the category either must be sub-divided or be given a definition based on principles other than enumeration.[1]
For example, for millennia we earthlings have had a cultural category of “planet” as a “wandering” celestial object, and because we only knew of planets in our own solar system, the planet category was defined by enumeration: Mercury, Venus, Earth, Mars, Jupiter, and Saturn. When the outer planets of Uranus, Neptune, and Pluto were identified as planets in the 18th-20th centuries, they were added to this list of planets without any changes in the cultural category. But in the last couple of decades many heretofore unknown planets outside our solar system have been detected, making the set of planets unbounded, and definition by enumeration no longer works.
The International Astronomical Union(IAU) thought it solved this category crisis by proposing a definition of planet as “a celestial body that is (a) in orbit around a star, (b) has sufficient mass for its self-gravity to overcome rigid body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, and (c) has cleared the neighborhood around its orbit.” Unfortunately, Pluto does not satisfy the third requirement, so it no longer is a member of the planet category, and instead is now called an “inferior planet.”
Changing the definition of a significant cultural category generated a great deal of controversy and angst among ordinary non-scientific people. A typical headline was “Pluto’s demotion has schools spinning,” describing the outcry from elementary school students and teachers about the injustice done to Pluto and the disruption on the curriculum. [2]
Single Properties
It is intuitive and useful to think in terms of properties when we identify instances and when we are describing instances (as we saw in “Resource Identity” and in Resource Description and Metadata). Therefore, it should also be intuitive and useful to consider properties when we analyze more than one instance to compare and contrast them so we can determine which sets of instances can be treated as a category or equivalence class. Categories whose members are determined by one or more properties or rules follow the principle of intensional definition, and the defining properties are called the intension.
You might be thinking here that enumeration or extensional definition of a category is also a property test; is not “being a state” a property of California? But statehood is not a property precisely because “state” is defined by extension, which means the only way to test California for statehood is to see if it is in the list of states.[3]
Any single property of a resource can be used to create categories, and the easiest ones to use are often the intrinsic static properties. As we discussed in Resource Description and Metadata, intrinsic static properties are those inherent in a resource that never change. The material of composition of natural or manufactured objects is an intrinsic and static property that can be used to arrange physical resources. For example, an organizing system for a personal collection of music that is based on the intrinsic static property of physical format might use categories for CDs, DVDs, vinyl albums, 8-track cartridges, reel-to-reel tape, and tape cassettes.[4]
Using a single property is most natural to do when the properties can take on only a small set of discrete values like music formats, and especially when the property is closely related to how the resources are used, as they are with the music collection where each format requires different equipment to listen to the music. Each value then becomes a subcategory of the music category.
The author, date, and location where an intellectual resource was created cannot be directly perceived but they are also intrinsic static properties. The subject matter or purpose of a resource, its “what it is about” or “what it was originally for,” are also intrinsic static properties that are not directly perceivable, especially for information resources.
The name or identifier of a resource is often arbitrary but once assigned normally does not change, making it an extrinsic static property. Any collection of resources with alphabetic or numeric identifiers as an associated property can use sorting order as an organizing principle to arrange spices, books, personnel records, etc., in a completely reliable way. Some might argue whether this organizing principle creates a category system, or whether it simply exploits the ordering inherent in the identifier notation. For example, with alphabetic identifiers, we can think of alphabetic ordering as creating a recursive category system with 26 (A-Z) top-level categories, each containing the same number of second-level categories, and so on until every instance is assigned to its proper place.[5]
Some resource properties are both extrinsic and dynamic because they are based on usage or behaviors that can be highly context-dependent. The current owner or location of a resource, its frequency of access, the joint frequency of access with other resources, or its current rating or preference with respect to alternative resources are typical extrinsic and dynamic properties that can be the basis for arranging resources and defining categories.
These properties can have a large number of values or are continuous measures, but as long as there are explicit rules for using property values to determine category assignment the resulting categories are still easy to understand and use. For example, we naturally categorize people we know on the basis of their current profession, the city where they live, their hobbies, or their age. Properties with a numerical dimension like “frequency of use” are often transformed into a small set of categories like “frequently used,” “occasionally used,” and “rarely used” based on the numerical property values.[6]
There is an infinite number of logically expressible properties for any resource, but most of them would not lead to categories that would be interpretable and useful for people. If people are going to use the categories, it is important to base them on properties that are psychologically or pragmatically relevant for the resource domain being categorized. Whether something weighs more or less than 5000 pounds is a poor property to apply to things in general, because it puts cats and chairs in one category, and buses and elephants in another.[7]
To summarize: The most useful single properties to use for creating categories for an organizing system used by people are those that are formally assigned, objectively measurable and orderable, or tied to well-established cultural categories, because the resulting categories will be easier to understand and describe.
If only a single property is used to distinguish among some set of resources and to create the categories in an organizing system, the choice of property is critical because different properties often lead to different categories. Using the age property, Bill Gates and Mark Zuckerberg are unlikely to end up in the same category of people. Using the wealth property, they most certainly would. Furthermore, if only one property is used to create a system of categories, any category with a large numbers of items in it will lack coherence because differences on other properties will be too apparent, and some category members will not fit as well as the others.
Multiple Properties
Organizing systems often use multiple properties to define categories. There are three different ways in which to do this that differ in the scope of the properties and how essential they are in defining the categories.
Multi-Level or Hierarchical Categories
If you have many shirts in your closet (and you are a bit compulsive or a “neat freak”), instead of just separating your shirts from your pants using a single property (the part of body on which the clothes are worn) you might arrange the shirts by style, and then by sleeve length, and finally by color. When all of the resources in an organizing system are arranged using the same sequence of resource properties, this creates a logical hierarchy, a multi-level category system.
If we treat all the shirts as the collection being organized, in the shirt organizing system the broad category of shirts is first divided by style into categories like “dress shirts,” “work shirts,” “party shirts,” and “athletic or sweatshirts.” Each of these style categories is further divided until the categories are very narrow ones, like the “white long-sleeve dress shirts” category. A particular shirt ends up in this last category only after passing a series of property tests along the way: it is a dress shirt, it has long sleeves, and it is white. Each test creates more precise categories in the intersections of the categories whose members passed the prior property tests.
Put another way, each subdivision of a category takes place when we identify or choose a property that differentiates the members of the category in a way that is important or useful for some intent or purpose. Shirts differ from pants in the value of the “part of body” property, and all the shirt subcategories share this “top part” value of that property. However, shirts differ on other properties that determine the subcategory to which they belong. Even as we pay attention to these differentiating properties, it is important to remember the other properties, the ones that members of a category at any level in the hierarchy have in common with the members of the categories that contain it. These properties are often described as “inherited” or “inferred” from the broader category.[8] For example, just as every shirt shares the “worn on top part of body” property, every item of clothing shares the “can be worn on the body” property, and every resource in the “shirts” and “pants” category inherits that property.
Each differentiating property creates another level in the category hierarchy, which raises an obvious question: How many properties and levels do we need? In order to answer this question, we must reflect upon the shirt categories in our closet. Our organizing system for shirts arranges them with the three properties of style, sleeve length, and color; some of the categories at the lowest level of the resulting hierarchy might have only one member, or no members at all. You might have yellow or red short-sleeved party shirts, but probably do not have yellow or red long-sleeved dress shirts, making them empty categories. Obviously, any category with only one member does not need any additional properties to tell the members apart, so a category hierarchy is logically complete if every resource is in a category by itself.
However, even when the lowest level categories of our shirt organizing system have more than one member, we might choose not to use additional properties to subdivide it because the differences that remain among the members do not matter to us for the interactions the organizing system needs to support. Suppose we have two long-sleeve white dress shirts from different shirt makers, but whenever we need to wear one of them, we ignore this property. Instead, we just pick one or the other, treating the shirts as completely equivalent or substitutable. When the remaining differences between members of a category do not make a difference to the users of the category, we can say that the organizing system is pragmatically or practically complete even if it is not yet logically complete. That is to say, it is complete “for all intents and purposes.” Indeed, we might argue that it is desirable to stop subdividing a system of categories while there are some small differences remaining among the items in each category because this leaves some flexibility or logical space in which to organize new items. This point might remind you of the concept of overfitting, where models with many parameters can very accurately fit their training data, but as a result generalize less well to new data. (See “Resource Description for Sensemaking and Science”.)
On the other hand, consider the shirt section of a big department store. Shirts there might be organized by style, sleeve length, and color as they are in our home closet, but would certainly be further organized by shirt maker and by size to enable a shopper to find a Marc Jacobs long-sleeve blue dress shirt of size 15/35. The department store organizing system needs more properties and a deeper hierarchy for the shirt domain because it has a much larger number of shirt instances to organize and because it needs to support many shirt shoppers, not just one person whose shirts are all the same size.
Different Properties for Subsets of Resources
A different way to use multiple resource properties to create categories in an organizing system is to employ different properties for distinct subsets of the resources being organized. This contrasts with the strict multi-level approach in which every resource is evaluated with respect to every property. Alternatively, we could view this principle as a way of organizing multiple domains that are conceptually or physically adjacent, each of which has a separate set of categories based on properties of the resources in that domain. This principle is used for most folder structures in computer file systems and by many email applications; you can create as many folder categories as you want, but any resource can only be placed in one folder.
The contrasts between intrinsic and extrinsic properties, and between static and dynamic ones, are helpful in explaining this method of creating organizing categories. For example, you might organize all of your clothes using intrinsic static properties if you keep your shirts, socks, and sweaters in different drawers and arrange them by color; extrinsic static properties if you share your front hall closet with a roommate, so you each use only one side of that closet space; intrinsic dynamic properties if you arrange your clothes for ready access according to the season; and, extrinsic dynamic properties if you keep your most frequently used jacket and hat on a hook by the front door.[9]
If we relax the requirement that different subsets of resources use different organizing properties and allow any property to be used to describe any resource, the loose organizing principle we now have is often called tagging. Using any property of a resource to create a description is an uncontrolled and often unprincipled principle for creating categories, but it is increasingly popular for organizing photos, web sites, email messages in gmail, or other web-based resources. We discuss tagging in more detail in “Tagging of Web-based Resources”.
Necessary and Sufficient Properties
A large set of resources does not always require many properties and categories to organize it. Some types of categories can be defined precisely with just a few essential properties. For example, a prime number is a positive integer that has no divisors other than 1 and itself, and this category definition perfectly distinguishes prime and not-prime numbers no matter how many numbers are being categorized. “Positive integer” and “divisible only by 1 and itself” are necessary or defining properties for the prime number category; every prime number must satisfy these properties. These properties are also sufficient to establish membership in the prime number category; any number that satisfies the necessary properties is a prime number. Categories defined by necessary and sufficient properties are also called monothetic. They are also sometimes called classical categories because they conform to Aristotle’s theory of how categories are used in logical deduction using syllogisms.[10] (See the sidebar, The Classical View of Categories.)
Theories of categorization have evolved a great deal since Plato and Aristotle proposed them over two thousand years ago, but in many ways we still adhere to classical views of categories when we create organizing systems because they can be easier to implement and maintain that way.
An important implication of necessary and sufficient category definition is that every member of the category is an equally good member or example of the category; every prime number is equally prime. Institutional category systems often employ necessary and sufficient properties for their conceptual simplicity and straightforward implementation in decision trees, database schemas,and programming language classes.
Consider the definition of an address as requiring a street, city, governmental region, and postal code. Anything that has all of these information components is therefore considered to be a valid address, and anything that lacks any of them will not be considered to be a valid address. If we refine the properties of an address to require the governmental region to be a state, and specifically one of the United States Postal Service’s list of official state and territory codes, we create a subcategory for US addresses that uses an enumerated category as part of its definition. Similarly, we could create a subcategory for Canadian addresses by exchanging the name “province” for state, and using an enumerated list of Canadian province and territory codes.
The Limits of Property-Based Categorization
Property-based categorization works tautologically well for categories like “prime number” where the category is defined by necessary and sufficient properties. Property-based categorization also works well when properties are conceptually distinct and the value of a property is easy to perceive and examine, as they are with man-made physical resources like shirts.
Historical experience with organizing systems that need to categorize information resources has shown that basing categories on easily perceived properties is often not effective. There might be indications “on the surface” that suggest the “joints” or boundaries between types of information resources, but these are often just presentation or packaging choices, That is to say, neither the size of a book nor the color of its cover are reliable cues for what it contains. Information resources have numerous descriptive properties like their title, author, and publisher that can be used more effectively to define categories, and these are certainly useful for some kinds of interactions, like finding all of the books written by a particular author or published by the same publisher. However, for practical purposes, the most useful property of an information resource is its aboutness, which may not be objectively perceivable and which is certainly hard to characterize.[11] Any collection of information resources in a library or document filing system is likely to be about many subjects and topics, and when an individual resource is categorized according to a limited number of its content properties, it is at the same time not being categorized using the others.
When the web first started, there were many attempts to create categories of web sites, most notably by Yahoo! As the web grew, it became obvious that search engines would be vastly more useful because their near real-time text indexes obviate the need for a priori assignment of web pages to categories. Rather, web search engines represent each web page or document in a way that treats each word or term they contain as a separate property.
Considering every distinct word in a document stretches our notion of property to make it very different from the kinds of properties we have discussed so far, where properties were being explicitly used by people to make decisions about category membership and resource organization. It is just not possible for people to pay attention to more than a few properties at the same time even if they want to, because that is how human perceptual and cognitive machinery works. But computers have no such limitations, and algorithms for information retrieval and machine learning can use huge numbers of properties, as we will see later in this chapter and in Classification: Assigning Resources to Categories and Interactions with Resources.
Probabilistic Categories and “Family Resemblance”
As we have seen, some categories can be precisely defined using necessary and sufficient features, especially when the properties that determine category membership are easy to observe and evaluate. Something is either a prime number or it isn’t. A person cannot be a registered student and not registered at the same time.
However, categorization based on explicit and logical consideration of properties is much less effective, and sometimes not even possible for domains where properties lack one or more of the characteristics of separability, perceptibility, and necessity. Instead, we need to categorize using properties in a probabilistic or statistical way to come up with some measure of resemblance or similarity between the resource to be categorized and the other members of the category.
Consider a familiar category like “bird.” All birds have feathers, wings, beaks, and two legs. But there are thousands of types of birds, and they are distinguished by properties that some birds have that other birds lack: most birds can fly, most are active in the daytime, some swim, some swim underwater; some have webbed feet. These properties are correlated or clustered, a consequence of natural selection that conveys advantages to particular configurations of characteristics, and there are many different clusters; birds that live in trees have different wings and feet than those that swim, and birds that live in deserts have different colorations and metabolisms that those that live near water. So instead of being defined by a single set of properties that are both necessary and sufficient, the bird category is defined probabilistically, which means that decisions about category membership are made by accumulating evidence from the properties that are more or less characteristic of the category.
Categories of information resources often have the same probabilistic character. The category of spam messages is suggested by the presence of particular words (beneficiary, pharmaceutical) but these words also occur in messages that are not spam. A spam classifier uses the probabilities of each word in a message in spam and non-spam contexts to calculate an overall likelihood that the message is spam.
There are three related consequences for categories when their characteristic properties have a probabilistic distribution:
-
The first is an effect of typicality or centrality that makes some members of the category better examples than others. Membership in probabilistic categories is not all or none, so even if they share many properties, an instance that has more of the characteristic properties will be judged as better or more typical.[12] Try to define “bird” and then ask yourself if all of the things you classify as birds are equally good examples of the category (look at the six birds in Family Resemblance and Typicality). This effect is also described as gradience in category membership and reflects the extent to which the most characteristic properties are shared.
-
A second consequence is that the sharing of some but not all properties creates what we call family resemblances among the category members; just as biological family members do not necessarily all share a single set of physical features but still are recognizable as members of the same family. This idea was first proposed by the 20th-century philosopher Ludwig Wittgenstein, who used “games” as an example of a category whose members resemble each other according to shifting property subsets.[13]
-
The third consequence, when categories do not have necessary features for membership, is that the boundaries of the category are not fixed; the category can be stretched and new members assigned as long as they resemble incumbent members. Personal video games and multiplayer online games like World of Warcraft did not exist in Wittgenstein’s time but we have no trouble recognizing them as games and neither would Wittgenstein, were he alive. Recall that in Foundations for Organizing Systems we pointed out that the cultural category of “library” has been repeatedly extended by new properties, as when Flickr is described as a web-based photo-sharing library. Categories defined by family resemblance or multiple and shifting property sets are termed polythetic.
We conclude that instead of using properties one at a time to assign category membership, we can use them in a composite or integrated way where together a co-occurring cluster of properties provides evidence that contributes to a similarity calculation. Something is categorized as an A and not a B if it is more similar to A’s best or most typical member rather than it is to B’s.[16]
Similarity
Similarity is a measure of the resemblance between two things that share some characteristics but are not identical. It is a very flexible notion whose meaning depends on the domain within which we apply it. Some people consider that the concept of similarity is itself meaningless because there must always be some basis, some unstated set of properties, for determining whether two things are similar. If we could identify those properties and how they are used, there would not be any work for a similarity mechanism to do.[17]
To make similarity a useful mechanism for categorization we have to specify how the similarity measure is determined. There are four psychologically-motivated approaches that propose different functions for computing similarity: feature- or property-based, geometry-based, transformational, and alignment- or analogy-based. The big contrast here is between models that represent items as sets of properties or discrete conceptual features, and those that assume that properties vary on a continuous metric space.[18]
Feature-based Models of Similarity
An influential model of feature-based similarity calculation is Amos Tversky’s contrast model, which matches the features or properties of two things and computes a similarity measure according to three sets of features:
-
those features they share,
-
those features that the first has that the second lacks, and
-
those features that the second has that the first lacks.
The similarity based on the shared features is reduced by the two sets of distinctive ones. The weights assigned to each set can be adjusted to explain judgments of category membership. Another commonly feature-based similarity measure is the Jaccard coefficient, the ratio of the common features to the total number of them. This simple calculation equals zero if there are no overlapping features and one if all features overlap. Jaccard’s measure is often used to calculate document similarity by treating each word as a feature.[19]
We often use a heuristic version of feature-based similarity calculation when we create multi-level or hierarchical category systems to ensure that the categories at each level are at the same level of abstraction or breadth. For example, if we were organizing a collection of musical instruments, it would not seem correct to have subcategories of “woodwind instruments,” “violins,” and “cellos” because the feature-based similarity among the categories is not the same for all pairwise comparisons among the categories; violins and cellos are simply too similar to each other to be separate categories given woodwinds as a category.
Geometric Models of Similarity
Geometric models are a type of similarity framework in which items whose property values are metric are represented as points in a multi-dimensional feature- or property-space. The property values are the coordinates, and similarity is calculated by measuring the distance between the items.
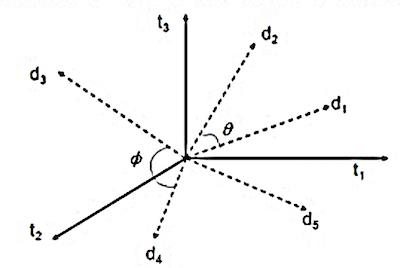
Geometric similarity functions are commonly used by search engines; if a query and document are each represented as a vector of search terms, relevance is determined by the distance between the vectors in the “term space.” The simplified diagram in the sidebar, Document Similarity, depicts four documents whose locations in the term space are determined by how many of each of three terms they contain. The document vectors are normalized to length 1, which makes it possible to use the cosine of the angle between any two documents as a measure of their similarity. Documents d1 and d2 are more similar to each other than documents d3 and d4, because angle between the former pair (Θ) is smaller than the angle between the latter (Φ). We will discuss how this works in greater detail in Interactions with Resources.
If the vectors that represent items in a multi-dimensional property space are of different lengths, instead of calculating similarity using cosines we need to calculate similarity in a way that more explicitly considers the differences on each dimension.
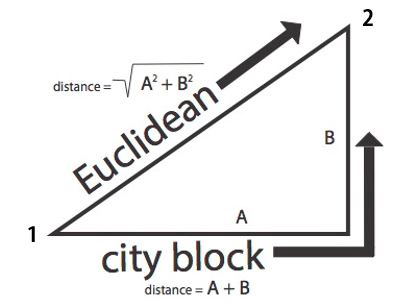
The diagram in the sidebar, Geometric Distance Functions shows two different ways of calculating the distance between points 1 and 2 using the differences A and B. The Euclidean distance function takes the square root of the sum of the squared differences on each dimension; in two dimensions, this is the familiar Pythagorean Theorem to calculate the length of the hypotenuse of a right triangle, where the exponent applied to the differences is 2. In contrast, the City Block distance function, so-named because it is the natural way to measure distances in cities with “gridlike” street plans, simply adds up the differences on each dimension, which is equivalent to an exponent of 1.
We can interpret the exponent as a weighting function that determines the relative contribution of each property to the overall distance or similarity calculation. The choice of exponent depends on the type of properties that characterize a domain and how people make category judgments within it. The exponent of 1 in the City Block function ensures that each property contributes its full amount. As the exponent grows larger, it magnifies the impact of the properties on which differences are the largest.
The Chebyshev function takes this to the limit (where the exponent would be infinity) and defines the distance between two items as the difference of their values on the single property with the greatest difference. What this means in practice is that two items could have similar or even identical values on most properties, but if they differ much on just one property, they will be treated as very dissimilar. We can make an analogy to stereotyping or prejudice when a person is just like you in all ways except for the one property you view as negative, which then becomes the only one that matters to you.
At the other extreme, if the exponent is reduced to zero, this treats each property as binary, either present or absent, and the distance function becomes a count of the number of times that the value of the property for one item is different from the value for the other one. This is called the “Hamming distance.”
Transformational Models of Similarity
Transformational models assume that the similarity between two things is inversely proportional to the complexity of the transformation required to turn one into the other. The simplest transformational model of similarity counts the number of properties that would need to change their values. More generally, one way to perform the name matching task of determining when two different strings denote the same person, object, or other named entity is to calculate the “edit distance” between them; the number of changes required to transform one into the other.
The simplest calculation just counts the number of insertion, deletion, and substitution operations and is called the Levenshtein distance; for example, the distance between “bob” and “book” is two: insert “o” and change the second “b” to “k”. Two strings with a short edit distance might be variant spellings or misspellings of the same name, and transformational models that are sensitive to common typing errors like transposed or duplicated letters are very effective at spelling correction. Transformational models of similarity are also commonly used to detect plagiarism and duplicate web pages.[20]
Alignment or Analogy Models of Similarity
None of the previous types of similarity models works very well when comparing things that have lots of internal or relational structure. In these cases, calculations based on matching features is insufficient; you need to compare features that align because they have the same role in structures or relationships. For example, a car with a green wheel and a truck with a green hood both share the feature green, but this matching feature does not increase their similarity much because the car’s wheel does not align with the truck’s hood. On the other hand, analogy lets us say that an atom is like the solar system. They have no common properties, but they share the relationship of having smaller objects revolving around a large one.
This kind of analogical comparison is especially important in problem solving. You might think that experts are good at solving problems in their domain of expertise because they have organized their knowledge and experience in ways that enable efficient search for and evaluation of possible solutions. For example, it is well known that chess masters search their memories of previous winning positions and the associated moves to decide what to play. However, top chess players also organize their knowledge and select moves on the basis of abstract similarities that cannot be explained in terms of specific positions of chess pieces. This idea that experts represent and solve problems at deeper levels than novices do by using more abstract principles or domain structure has been replicated in many areas. Novices tend to focus more on surface properties and rely more on literal similarity.[21]
Goal-Derived Categories
Another psychological principle for creating categories is to organize resources that go together in order to satisfy a goal. Consider the category “Things to take from a burning house,” an example that cognitive scientist Lawrence Barsalou termed an ad hoc or goal-derived category.[22]
What things would you take from your house if a fire threatened it?? Possibly your cat, your wallet and checkbook, important papers like birth certificates and passports, and grandma’s old photo album, and anything else you think is important, priceless, or irreplaceable—as long as you can carry it. These items have no discernible properties in common, except for being your most precious possessions. The category is derived or induced by a particular goal in some specified context.
Theory-Based Categories
A final psychological principle for creating categories is organizing things in ways that fit a theory or story that makes a particular categorization sensible. A theory-based category can win out even if probabilistic categorization, on the basis of family resemblance or similarity with respect to visible properties, would lead to a different category assignment. For example, a theory of phase change explains why liquid water, ice, and steam are all the same chemical compound even though they share few visible properties.
Theory-based categories based on origin or causation are especially important with highly inventive and computational resources because unlike natural kinds of physical resources, little or none of what they can do or how they behave is visible on the surface (see “Affordance and Capability”). Consider all of the different appearances and form factors of the resources that we categorize as “computers” —their essence is that they all compute, an invisible or theory-like principle that does not depend on their visible properties.[23]
-
Legal disputes often reflect different interpretations of category membership and whether a list of category members is exhaustive or merely illustrative. The legal principle of “implied exclusion”—expressio unius est exclusio alterius —says that if you “expressly name” or “designate” an enumeration of one or more things, any thing that is not named is excluded, by implication. However, prefacing the list with “such as,” “including,” or “like” implies that it is not a strict enumeration because there might be other members.
-
International Astronomical Union(IAU) (iau.org) published its new definition of planet in August 2006. A public television documentary in 2011 called The Pluto Files retells the story (Tyson 2011).
-
The distinction between intension and extension was introduced by Gottlob Frege, a German philosopher and mathematician (Frege 1892).
-
The number of resources in each of these categories depends on the age of the collection and the collector. We could be more precise here and say “single atomic property” or otherwise more carefully define “property” in this context as a characteristic that is basic and not easily or naturally decomposable into other characteristics. It would be possible to analyze the physical format of a music resource as a composition of size, shape, weight, and material substance properties, but that is not how people normally think. Instead, they treat physical format as a single property as we do in this example.
-
We need to think of alphabetic ordering or any other organizing principle in a logical way that does not imply any particular physical implementation. Therefore, we do not need to consider which of these alphabetic categories exist as folders, files, or other tangible partitions.
-
Another example: rules for mailing packages might use either size or weight to calculate the shipping cost, and whether these rules are based on specific numerical values or ranges of values, the intent seems to be to create categories of packages.
-
If you try hard, you can come up with situations in which this property is important, as when the circus is coming to the island on a ferry or when you are loading an elevator with a capacity limit of 5000 pounds, but it just is not a useful or psychologically salient property in most contexts.
-
Many information systems, applications, and programming languages that work with hierarchical categories take advantage of this logical relationship to infer inherited properties when they are needed rather than storing them redundantly.
-
Similarly, clothing stores use intrinsic static properties when they present merchandise arranged according to color and size; extrinsic static properties when they host branded displays of merchandise; intrinsic dynamic properties when they set aside a display for seasonal merchandise, from bathing suits to winter boots; and extrinsic dynamic properties when a display area is set aside for “Today’s Special.”
-
Aristotle did not call them classical categories. That label was bestowed about 2300 years later by (Smith and Medin 1981).
-
We all use the word “about” with ease in ordinary discourse, but “aboutness” has generated a surprising amount of theoretical commentary about its typically implicit definition, starting with (Hutchins 1977) and (Maron 1977) and relentlessly continued by (Hjørland 1992, 2001).
-
Typicality and centrality effects were studied by Rosch and others in numerous highly influential experiments in the 1970s and 1980s (Rosch 1975). Good summaries can be found in (Mervis and Rosch 1981), (Rosch 1999), and in Chapter 1 of (Rogers and McClelland 2008).
-
An easy to find source for Wittgenstein’s discussion of “game” is (Wittgenstein 2002) in a collection of core readings for cognitive psychology (Levitin 2002).
-
The philosopher’s poll that ranked Wittgenstein’s book #1 is reported by (Lackey 1999).
-
It might be possible to define “game,”but it requires a great deal of abstraction that obscures the “necessary and sufficient” tests. “To play a game is to engage in activity directed toward bringing about a specific state of affairs, using only means permitted by specific rules, where the means permitted by the rules are more limited in scope than they would be in the absence of the rules, and where the sole reason for accepting such limitation is to make possible such activity.” (Suits 1967)
-
The exact nature of the category representation to which the similarity comparison is made is a subject of ongoing debate in cognitive science. Is it a prototype, a central tendency or average of the properties shared by category members, or it one or more exemplars, particular members that typify the category. Or is it neither, as argued by connectionist modelers who view categories as patterns of network activation without any explicitly stored category representation? Fortunately, these distinctions do not matter for our discussion here. A recent review is (Rips, Smith, and Medin 2012).
-
Another situation where similarity has been described as a “mostly vacuous” explanation for categorization is with abstract categories or metaphors. Goldstone says “an unrewarding job and a relationship that cannot be ended may both be metaphorical prisons... and may seem similar in that both conjure up a feeling of being trapped... but this feature is almost as abstract as the category to be explained.” (Goldstone 1994), p. 149.
-
(Medin, Goldstone, and Gentner 1993) and (Tenenbaum and Griffiths 2001).
-
Because Tversky's model separately considers the sets of non-overlapping features, it is possible to accurately capture similarity judgments when they are not symmetric, i.e., when A is judged more similar to B than B is to A. This framing effect is well-established in the psychological literature and many machine learning algorithms now employ asymmetric measures. (Tversky 1974)
-
For a detailed explanation of distance and transformational models of similarity, see (Flach 2012), Chapter 9. There are many online calculators for Levenshein distance; http://www.let.rug.nl/kleiweg/lev/ also has a compelling visualization. The “strings” to be matched can themselves be transformations. The “soundex” function is very commonly used to determine if two words could be different spellings of the same name. It “hashes” the names into phonetic encodings that have fewer characters than the text versions. See (Christen 2006) and
http://www.searchforancestors.com/utility/soundex.htmlto try it yourself. -
This explanation for expert-novice differences in categorization and problem solving was proposed in (Chi et al 1981). See (Linhares 2007) for studies of abstract reasoning by chess experts.
-
The emergence of theory-based categorization is an important event in cognitive development that has been characterized as a shift from “holistic” to “analytic” categories or from “surface properties” to “principles.” See (Carey and Gelman 1991) (Rehder and Hastie 2004).