49 Implementing Categories
Categories are conceptual constructs that we use in a mostly invisible way when we talk or think about them. When we organize our kitchens, closets, or file cabinets using shelves, drawers, and folders, these physical locations and containers are visible implementations of our personal category system, but they are not the categories. This distinction between category design and implementation is obvious when we follow signs and labels in libraries or grocery stores to find things, search a product catalog or company personnel directory, or analyze a set of economic data assembled by the government from income tax forms. These institutional categories were designed by people prior to the assignment of resources to them.
This separation between category creation and category implementation prompts us to ask how a system of categories can be implemented. We will not discuss the implementation of categories in the literal sense of building physical or software systems that organize resources. Instead, we will take a higher-level perspective that analyzes the implementation problem to be solved for the different types of categories discussed in “Principles for Creating Categories”, and then explain the logic followed to assign resources correctly to them.
Implementing Enumerated Categories
Categories defined by enumeration are easy to implement. The members or legal values in a set define the category, and testing an item for membership means looking in the set for it. Enumerated category definitions are familiar in drop-down menus and form-filling. You scroll through a list of all the countries in the world to search for the one you want in a shipping address, and whatever you select will be a valid country name, because the list is fixed until a new country is born. Enumerated categories can also be implemented with associative arrays (also known as hash tables or dictionaries). With these data structures, a test for set membership is even more efficient than searching, because it takes the same time for sets of any size (see “Kinds of Structures”).
Implementing Categories Defined by Properties
The most conceptually simple and straightforward implementation of categories defined by properties adopts the classical view of categories based on necessary and sufficient features. Because such categories are prescriptive with explicit and clear boundaries, classifying items into the categories is objective and deterministic, and supports a well-defined notion of validation to determine unambiguously whether some instance is a member of the category. Items are classified by testing them to determine if they have the required properties and property values. Tests can be expressed as rules:
-
If instance X has property P, then X is in category Y.
-
If a home mortgage loan in San Francisco exceeds $625,000, then it is classified as a “jumbo” loan by the US Office of Federal Housing Oversight.
-
For a number to be classified as prime it must satisfy two rules: It must be greater than 1, and have no positive divisors other than 1 and itself.
This doesn’t mean the property test is always easy; validation might require special equipment or calculations, and tests for the property might differ in their cost or efficiency. But given the test results, the answer is unambiguous. The item is either a member of the category or it isn’t.[1]
A system of hierarchical categories is defined by a sequence of property tests in a particular order. The most natural way to implement multi-level category systems is with decision trees. A simple decision tree is an algorithm for determining a decision by making a sequence of logical or property tests. Suppose a bank used a sequential rule-based approach to decide whether to give someone a mortgage loan.
-
If an applicant’s annual income exceeds $100,000, and if the monthly loan payment is less than 25% of monthly income, approve the mortgage application.
-
Otherwise, deny the loan application.
This simple decision tree is depicted in Figure: Rule-based Decision Tree. The rules used by the bank to classify loan applications as “Approved” or “Denied” have a clear representation in the tree. The easy interpretation of decision trees makes them a common formalism for implementing classification models.
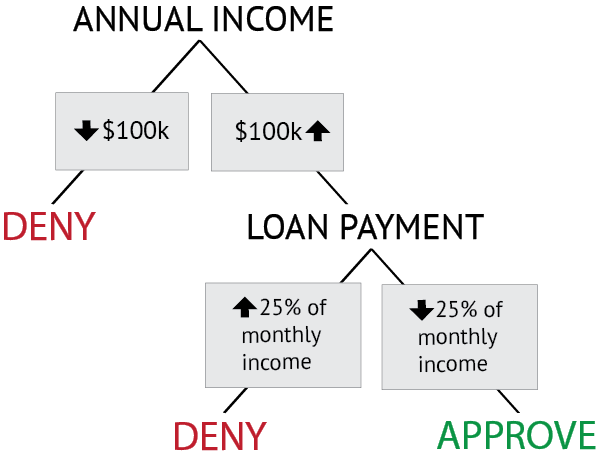
In this simple decision tree, a sequence of two tests for the borrower’s annual income and the percentage of monthly income required to make the loan payment classify the applicants into the “deny” and “approve” categories.
Nevertheless, any implementation of a category is only interpretable to the extent that the properties and tests it uses in its definition and implementation can be understood. Because natural language is inherently ambiguous, it is not the optimal representational format for formally defined institutional categories. Categories defined using natural language can be incomplete, inconsistent, or ambiguous because words often have multiple meanings. This implementation of the bank’s procedure for evaluating loans would be hard to interpret reliably:
-
If applicant is wealthy, and then if the monthly payment is an amount that the applicant can easily repay, then applicant is approved.
To ensure their interpretability, decision trees are sometimes specified using the controlled vocabularies and constrained syntax of “simplified writing” or “business rule” systems.
Artificial languages are a more ambitious way to enable precise specification of property-based categories. An artificial language expresses ideas concisely by introducing new terms or symbols that represent complex ideas along with syntactic mechanisms for combining and operating on them. Mathematical notation, programming languages, schema languages that define valid document instances (see “Specifying Vocabularies and Schemas”), and regular expressions that define search and selection patterns (see “Controlling Values”) are familiar examples of artificial languages. It is certainly easier to explain and understand the Pythagorean Theorem when it is efficiently expressed as “H2 = A2 + B2” than with a more verbose natural language expression: “In all triangles with an angle such that the sides forming the angle are perpendicular, the product of the length of the side opposite the angle such that the sides forming the angle are perpendicular with itself is equal to the sum of the products of the lengths of the other two sides, each with itself.”[2]
Artificial languages for defining categories have a long history in philosophy and science. (See the sidebar, Artificial Languages for Description and Classification). However, the vast majority of institutional category systems are still specified with natural language, despite its ambiguities because people usually understand the languages they learned naturally better than artificial ones. Sometimes this is even intentional to allow institutional categories embodied in laws to evolve in the courts and to accommodate technological advances.[3]
Data schemas that specify data entities, elements, identifiers, attributes, and relationships in databases and XML document types on the transactional end of the Document Type Spectrum (“Resource Domain”) are implementations of the categories needed for the design, development and maintenance of information organization systems. Data schemas tend to rigidly define categories of resources. [5]
In object-oriented programming languages, classes are schemas that serve as templates for the creation of objects. A class in a programming language is analogous to a database schema that specifies the structure of its member instances, in that the class definition specifies how instances of the class are constructed in terms of data types and possible values. Programming classes may also specify whether data in a member object can be accessed, and if so, how.[6]
Unlike transactional document types, which can be prescriptively defined as classical categories because they are often produced and consumed by automated processes, narrative document types are usually descriptive in character. We do not classify something as a novel because it has some specific set of properties and content types. Instead, we have a notion of typical novels and their characteristic properties, and some things that are considered novels are far from typical in their structure and content.[7]
Nevertheless, categories like narrative document types can sometimes be implemented using document schemas that impose only a few constraints on structure and content. A schema for a purchase order is highly prescriptive; it uses regular expressions, strongly data typed content, and enumerated code lists to validate the value of required elements that must occur in a particular order. In contrast, a schema for a narrative document type would have much optionality, be flexible about order, and expect only text in its sections, paragraphs and headings. Even very lax document schemas can be useful in making content management, reuse, and formatting more efficient.
Implementing Categories Defined by Probability and Similarity
Many categories cannot be defined in terms of required properties, and instead must be defined probabilistically, where category membership is determined by properties that resources are likely to share. Consider the category “friend.” You probably consider many people to be your friends, but you have longtime friends, school friends, workplace friends, friends you see only at the gym, and friends of your parents. Each of these types of friends represents a different cluster of common properties. If someone is described to you as a potential friend or date, how accurately can you predict that the person will become a friend? (See the sidebar, Finding Friends and Dates: Lessons for Learning Categories)
Probabilistic categories can be challenging to define and use because it can be difficult to keep in mind the complex feature correlations and probabilities exhibited by different clusters of instances from some domain. Furthermore, when the category being learned is broad with a large number of members, the sample from which you learn strongly shapes what you learn. For example, people who grow up in high-density and diverse urban areas may have less predictable ideas of what an acceptable potential date looks like than someone in a remote rural area with a more homogeneous population.
More generally, if you are organizing a domain where the resources are active, change their state, or are measurements of properties that vary and co-occur probabilistically, the sample you choose strongly affects the accuracy of models for classification or prediction. In The Signal and the Noise, statistician Nate Silver explains how many notable predictions failed because of poor sampling techniques. One common sampling mistake is to use too short a historical window to assemble the training dataset; this is often a corollary of a second mistake, an over reliance on recent data because it is more available. For example, the collapse of housing prices and the resulting financial crisis of 2008 can be explained in part because the models that lenders used to predict mortgage foreclosures were based on data from 1980-2005, when house prices tended to grow higher. As a result, when mortgage foreclosures increased rapidly, the results were “out of sample” and were initially misinterpreted, delaying responses to the crisis.
Samples from dynamic and probabilistic domains result in models that capture this variability. Unfortunately, because many forecasters want to seem authoritative, and many people do not understand probability, classifications or predictions that are inherently imprecise are often presented with certainty and exactness even though they are probabilistic with a range of outcomes. Silver tells the story of a disastrous 1997 flood caused when the Red River crested at 54 feet when the levees protecting the town of Grand Forks were at 51 feet. The weather service had predicted a crest between 40 and 58 feet, but emphasized the midpoint of the range, which was 49 feet. Unfortunately, most people interpreted this probabilistic prediction as if it were a binary classification, “flood” versus “no flood,” ignored the range of the forecast, and failed to prepare for a flood that had about a 35% chance of occurring.[8]
Probabilistic Decision Trees
In “Implementing Categories Defined by Properties”, we showed how a rule-based decision tree could be used to implement a strict property-based classification in which a bank uses tests for the properties of “annual income” and “monthly loan payment” to classify applicants as approved or denied. We can adapt that example to illustrate probabilistic decision trees, which are better suited for implementing categories in which category membership is probabilistic rather than absolute.
Banks that are more flexible about making loans can be more profitable because they can make loans to people that a stricter bank would reject but who still are able to make loan payments. Instead of enforcing conservative and fixed cutoffs on income and monthly payments, these banks consider more properties and look at applications in a more probabilistic way. These banks recognize that not every loan applicant who is likely to repay the loan looks exactly the same; “annual income” and “monthly loan payment” remain important properties, but other factors might also be useful predictors, and there is more than one configuration of values that an applicant could satisfy to be approved for a loan.
Which properties of applicants best predict whether they will repay the loan or default? A property that predicts each at 50% isn’t helpful because the bank might as well flip a coin, but a property that splits the applicants into two sets, each with very different probabilities for repayment and defaulting, is very helpful in making a loan decision.
A data-driven bank relies upon historical data about loan repayment and defaults to train algorithms that create decision trees by repeatedly splitting the applicants into subsets that are most different in their predictions. Subsets of applicants with a high probability of repayment would be approved, and those with a high probability of default would be denied a loan. One method for selecting the property test for making each split is calculating the “information gain” (see the sidebar Using “Information Theory” to Quantify Organization). This measure captures the degree to which each subset contains a “pure” group in which every applicant is classified the same, as likely repayers or likely defaulters.
For example, consider the chart in Figure: Historical Data: Loan Repayment Based on Interest Rate which is a simplified representation of the bank’s historical data on loan defaults based on the initial interest rate. The chart represents loans that were repaid with “o” and those that defaulted with “x.” Is there an interest rate that divides them into “pure” sets, one that contains only “o” loans and the other that contains only “x” loans?
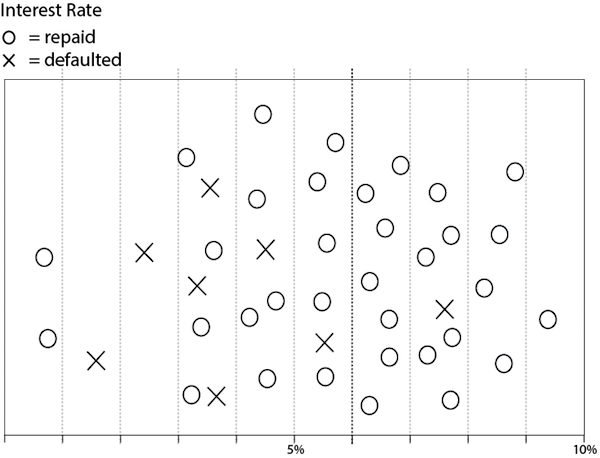
The “o” symbol represents loans that were repaid by the borrower; “x” represents loans on which the borrower defaulted. A 6% rate (darker vertical line) best divides the loans into subsets that differ in the payment outcome.
You can see that no interest rate divides these into pure sets. So the best that can be done is to find the interest rate that divides them so that the proportions of defaulters are most different on each side of the line.[9]
This dividing line at the 6% interest rate best divides those who defaulted from those who repaid their loan. Most people who borrowed at 6% or greater repaid the loan, while those who took out loans at a lower rate were more likely to default. This might seem counter-intuitive until you learn that the lower-interest rate loans had adjustable rates that increased after a few years, causing the monthly payments to increase substantially. More prudent borrowers were willing to pay higher interest rates that were fixed rather than adjustable to avoid radical increases in their monthly payments.
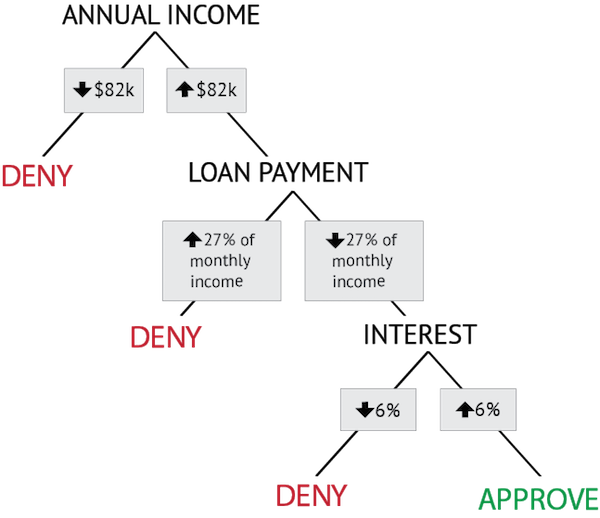
In this probabilistic decision tree, the sequence of property tests and the threshold values in each test divide the loan applicants into categories that differ in how likely they are to repay the loan.
This calculation is carried out for each of the attributes in the historical data set to identify the one that best divides the applicants into the repaid and defaulted categories. The attributes and the value that defines the decision rule can then be ordered to create a decision tree similar to the rule-based one we saw in “Implementing Categories Defined by Properties”. In our hypothetical case, it turns out that the best order in which to test the properties is Income, Monthly Payment, and Interest Rate, as shown in Figure: Probabilistic Decision Tree. The end result is still a set of rules, but behind each decision in the tree are probabilities based on historical data that can more accurately predict whether an applicant will repay or default. Thus, instead of the arbitrary cutoffs at $100,000 in income and 25% for monthly payment, the bank can offer loans to people with lower incomes and remain profitable doing so, because it knows from historical data that $82,000 and 27% are the optimal decision points. Using the interest rate in their decision process is an additional test to ensure that people can afford to make loan payments even if interest rates go up.[10]
Because decision trees specify a sequence of rules that make property tests, they are highly interpretable, which makes them a very popular choice for data scientists building models much more complex than the simple loan example here. But they assume that every class is a conjunction of all the properties used to define them. This makes them susceptible to over-fitting because if they grow very deep with many property conjunctions, they capture exactly the properties that describe each member of the training set, effectively memorizing the training data. In other words, they capture both what is generally true beyond the set and what is particular to the training set only, when the goal is to build a model that captures only what is generally true. Overfitting in decision trees can be prevented by pruning back the tree after it has perfectly classified the training set, or by limiting the depth of the tree in advance, essentially pre-pruning it.
Naïve Bayes Classifiers
Another commonly used approach to implement a classifier for probabilistic categories is called Naïve Bayes. It employs Bayes’ Theorem for learning the importance of a particular property for correct classification. There are some common sense ideas that are embodied in Bayes’ Theorem:
-
When you have a hypothesis or prior belief about the relationship between a property and a classification, new evidence consistent with that belief should increase your confidence.
-
Contradictory evidence should reduce confidence in your belief.
-
If the base rate for some kind of event is low, do not forget that when you make a prediction or classification for a new specific instance. It is easy to be overly influenced by recent information.
Now we can translate these ideas into calculations about how learning takes place. For property A and classification B, Bayes’ Theorem says:
P (A | B) = P (B|A) P(A) / P(B)
The left hand side of the equation, P (A | B), is what we want to estimate but can’t measure directly: the probability that A is the correct classification for an item or observation that has property B. This is called the conditional or posterior probability because it is estimated after seeing the evidence of property B.
P (B | A) is the probability that any item correctly classified as A has property B. This is called the likelihood function.
P (A) and P (B) are the independent or prior probabilities of A and B; what proportion of the items are classified as A? How often does property B occur in some set of items?
Your personal library contains 60% fiction and 40% nonfiction books. All of the fiction books are in ebook format, and half of the nonfiction books are ebooks and half are in print format. If you pick a book at random and it is in ebook format, what is the probability that it is nonfiction?
Bayes’ Theorem tells us that:
P (nonfiction | ebook) = P (ebook |nonfiction) x P (nonfiction) / P (ebook).
We know: P (ebook | nonfiction) = .5 and P (nonfiction) = .4
We compute P (ebook) using the law of total probability to compute the combined probability of all the independent ways in which an ebook might be sampled. In this example there are two ways:
P (ebook) = P (ebook | nonfiction) x P (nonfiction)
+ P (ebook | fiction) x P (fiction)
= (.5 x .4) + (1 x .6) = .8
Therefore: P (nonfiction | ebook) = (.5 x .4) / .8 = .25
Now let’s apply Bayes’ Theorem to implement email spam filtering. Messages are classified as SPAM or HAM (i.e., non-SPAM); the former are sent to a SPAM folder, while the latter head to your inbox.
-
Select Properties. We start with a set of properties, some from the message metadata like the sender’s email address or the number of recipients, and some from the message content. Every word that appears in messages can be treated as a separate property[11]
-
Assemble Training Data. We assemble a set of email message that have been correctly assigned to the SPAM and HAM categories. These labeled instances make up the training set.
-
Analyze the Training Data. For each message, does it contain a particular property? For each message, is it classified as SPAM? If a message is classified as SPAM, does it contain a particular property? (These are the three probabilities on the right side of the Bayes equation).
-
Learn. The conditional probability (the left side of the Bayes equation) is recalculated, adjusting the predictive value of each property. Taken together, all of the properties are now able to correctly assign (most of) the messages into the categories they belonged to in the training set.
-
Classify. The trained classifier is now ready to classify uncategorized messages to the SPAM or HAM categories.
-
Improve. The classifier can improve its accuracy if the user gives it feedback by reclassifying SPAM messages as HAM ones or vice versa. The most efficient learning occurs when an algorithm uses “active learning” techniques to choose its own training data by soliciting user feedback only where it is uncertain about how to classify a message. For example, the algorithm might be confident that a message with “Cheap drugs” in the subject line is SPAM, but if the message comes from a longtime correspondent, the algorithm might ask the user to confirm that the classification.[12]
Categories Created by Clustering
In the previous two sections, we discussed how probabilistic decision trees and naïve Bayes classifiers implement categories that are defined by typically shared properties and similarity. Both are examples of supervised learning because they need correctly classified examples as training data, and they learn the categories they are taught.
In contrast, clustering techniques are unsupervised; they analyze a collection of uncategorized resources to discover statistical regularities or structure among the items, creating a set of categories without any labeled training data.
Clustering techniques share the goal of creating meaningful categories from a collection of items whose properties are hard to directly perceive and evaluate, which implies that category membership cannot easily be reduced to specific property tests and instead must be based on similarity. For example, with large sets of documents or behavioral data, clustering techniques can find categories of documents with the same topics, genre, or sentiment, or categories of people with similar habits and preferences.
Because clustering techniques are unsupervised, they create categories based on calculations of similarity between resources, maximizing the similarity of resources within a category and maximizing the differences between them. These statistically-learned categories are not always meaningful ones that can be named and used by people, and the choice of properties and methods for calculating similarity can result in very different numbers and types of categories. Some clustering techniques for text resources suggest names for the clusters based on the important words in documents at the center of each cluster. However, unless there is a labeled set of resources from the same domain that can be used as a check to see if the clustering discovered the same categories, it is up to the data analyst or information scientist to make sense of the discovered clusters or topics.
There are many different distance-based clustering techniques, but they share three basic methods.
-
The first shared method is that clustering techniques start with an initially uncategorized set of items or documents that are represented in ways that enable measures of inter-item similarity can be calculated. This representation is most often a vector of property values or the probabilities of different properties so that items can be represented in a multidimensional space and similarity calculated using a distance function like those described in “Geometric Models of Similarity”.[13]
-
The second shared method is that categories are created by putting items that are most similar into the same category. Hierarchical clustering approaches start with every item in its own category. Other approaches, notably one called “K-means clustering,” start with a fixed number of K categories initialized with a randomly chosen item or document from the complete set.
-
The third shared method is refining the system of categories by iterative similarity recalculation each time an item is added to a category. Approaches that start with every item in its own category create a hierarchical system of categories by merging the two most similar categories, recomputing the similarity between the new category and the remaining ones, and repeating this process until all the categories are merged into a single category at the root of a category tree. Techniques that start with a fixed number of categories do not create new ones but instead repeatedly recalculate the “centroid” of the category by adjusting its property representation to the average of all its members after a new member is added.[14]
It makes sense that the algorithms that create clusters or categories of similar items can be later used as classifiers by using the same similarity measures to compare the unclassified items against items that are labeled by category. There are different choices about which items to compare with the unclassified one:
-
The centroid: a prototypical or average item calculated on the properties of all the category members. However, the centroid might not correspond to any actual member (see the sidebar Median versus Average), and this can make it hard to interpret the classification.
-
Items that actually exist: Because the items in categories defined by similarity are not equally typical or good members, it is more robust to test against more than one exemplar. Classifiers that use this approach are called nearest-neighbor techniques, and they essentially vote among themselves and the majority category is assigned to the new item.
-
The edge cases: These are instances that are closest to the boundary between two categories, so there needs to be at least two of them, one in each category. Because they are not typical members of the category, they are the hardest to classify initially, but using them in classifiers emphasizes the properties that are the most discriminating. This is the approach taken by support vector machines, which are not clustering algorithms but are somewhat like nearest-neighbor algorithms in that they calculate the similarity of an unclassified item to these edge cases. Their name makes more sense if you think of the vectors that represent the “edge cases” being used to “support” the category boundary, which falls between them.
Neural networks
Among the best performing classifiers for categorizing by similarity and probabilistic membership are those implemented using neural networks, and especially those employing deep learning techniques. Deep learning algorithms can learn categories from labeled training data or by using autoencoding, an unsupervised learning technique that trains a neural network to reconstruct its input data. However, instead of using the properties that are defined in the data, deep learning algorithms devise a very large number of features in hidden hierarchical layers, which makes them uninterpretable by people. The key idea that made deep learning possible is the use of “backpropagation” to adjust the weights on features by working backwards from the output (the object classification produced by the network) all the way back to the input. The use of deep learning to classify images was mentioned in “Describing Images”.[15]
Implementing Goal-Based Categories
Goal-based categories are highly individualized, and are often used just once in a very specific context. However, it is useful to consider that we could implement model goal-derived categories as rule-based decision trees by ordering the decisions to ensure that any sub-goals are satisfied according to their priority. We could understand the category “Things to take from a burning house” by first asking the question “Are there living things in the house?” because that might be the most important sub-goal. If the answer to that question is “yes,” we might proceed along a different path than if the answer is “no.” Similarly, we might put a higher priority on things that cannot be replaced (Grandma’s photos) than those that can (passport).
Implementing Theory-Based Categories
Theory-based categories arise in domains in which the items to be categorized are characterized by abstract or complex relationships with their features and with each other. With this model an entity need not be understood as inherently possessing features shared in common with another entity. Rather, people project features from one thing to another in a search for congruities between things, much as clue receivers in the second round of the Pyramid game search for congruities between examples provided by the clue giver in order to guess the target category. For example, a clue like “screaming baby” can suggest many categories, as can “parking meter.” But the likely intersection of the interactions one can have with babies and parking meters is that they are both “Things you need to feed.”
Theory-based categories are created as cognitive constructs when we use analogies and classify because things brought together by analogy have abstract rather than literal similarity. The most influential model of analogical processing is Structure Mapping, whose development and application have been guided by Dedre Gentner for over three decades.
The key insight in Structure Mapping is that an analogy “a T is like B” is created by matching relational structures and not properties between the base domain B and a target domain T. We take any two things, analyze the relational structures they contain, and align them to find correspondences between them. The properties of objects in the two domains need not match, and in fact, if too many properties match analogy goes away and we have literal similarity:
-
Analogy: The hydrogen atom is like our solar system
-
Literal Similarity: The X12 star system in the Andromeda galaxy is like our solar system
Structure Mapping theory was implemented in the Structure-Mapping Engine (SME), which both formalized the theory and offered a computationally-tractable algorithm for carrying out the process of mapping structures and drawing inferences.[16]
-
For example, you can test whether a number is prime by dividing it by every number smaller than its square root, but this algorithm is ridiculously impractical for any useful application. Many cryptographic systems multiply prime numbers to create encryption keys, counting on the difficulty of factoring them to protect the keys; so, proving that ever larger numbers are prime is very important. See (Crandall and Pomerance 2006).
If you are wondering why prime numbers aren’t considered an enumerative category given that every number that is prime already exists, it is because we have not found all of them yet, and we need to test through to infinity.
-
This example comes from (Perlman 1984), who introduced the idea of “natural artificial languages” as those designed to be easy to learn and use because they employ mnemonic symbols, suggestive names, and consistent syntax.
-
When the US Congress revised copyright law in 1976 it codified a “fair use” provision to allow for some limited uses of copyrighted works, but fair use in the digital era is vastly different today; website caching to improve performance and links that return thumbnail versions of images are fair uses that were not conceivable when the law was written. A law that precisely defined fair uses using contemporary technology would have quickly become obsolete, but one written more qualitatively to enable interpretation by the courts has remained viable. See (Samuelson 2009).
-
“Rigid” might sound negative, but a rigidly defined resource is also precisely defined. Precise definition is essential when creating, capturing, and retrieving data and when information about resources in different organizing systems needs to be combined or compared. For example, in a traditional relational database, each table contains a field, or combination of fields, known as a primary key, which is used to define and restrict membership in the table. A table of email messages in a database might define an email message as a unique combination of sender address, recipient address, and date/time when the message was sent, by enforcing a primary key on a combination of these fields. Similar to category membership based on a single, monothetic set of properties, membership in this email message table is based on a single set of required criteria. An item without a recipient address cannot be admitted to the table. In categorization terms, the item is not a member of the “email message” class because it does not have all the properties necessary for membership.
-
Like data schemas, programming classes specify and enforce rules in the construction and manipulation of data. However, programming classes, like other implementations that are characterized by specificity and rule enforcement, can vary widely in the degree to which rules are specified and enforced. While some class definitions are very rigid, others are more flexible. Some languages have abstract types that have no instances but serve to provide a common ancestor for specific implemented types.
-
The existence of chapters might suggest that an item is a novel; however, a lack of chapters need not automatically indicate that an item is not a novel. Some novels are hypertexts that encourage readers to take alternative paths. Many of the writings by James Joyce and Samuel Beckett are “stream of consciousness” works that lack a coherent plot, yet they are widely regarded as novels.
-
See (Silver 2012). Over reliance on data that is readily available is a decision-making heuristic proposed by (Tversky and Kahneman 1974), who developed the psychological foundations for behavioral economics. (See the sidebar, Behavioral Economics.)
-
To be precise, this “difference of proportions” calculation uses an algorithm that also uses the logarithm of the proportions to calculate entropy, a measure of the uncertainty in a probability distribution. An entropy of zero means that the outcome can be perfectly predicted and entropy increases as outcomes are less predictable. The information gain for an attribute is how much it reduces entropy after it is used to subdivide a dataset.
-
Unfortunately, this rational data-driven process for classifying loan applications as “Approved” or “Denied” was abandoned during the “housing bubble” of the early 2000s. Because lending banks could quickly sell their mortgages to investment banks who bundled them into mortgage-backed securities, applicants were approved without any income verification for “subprime” loans that initially had very low adjustable interest rates. Of course, when the rates increased substantially a few years later, defaults and foreclosures skyrocketed. This sad story is told in an informative, entertaining, but depressing manner in “The Big Short” (Lewis, 2010) and in a 2015 movie with the same name.
-
Machine learning algorithms differ in which properties they use in how they select them. A straightforward method is to run the algorithms using different sets of properties, and select the set that yields the best result. However, it can be very computationally expensive to run algorithms multiple times, especially when the number of properties is large. A faster alternative is to select or filter features based on how well they predict the classification. The information gain calculation discussed in “Probabilistic Decision Trees” is an example of a filter method.
Naïve Bayes classifiers make the simplifying assumption that the properties are independent, an assumption that is rarely correct, which is why the approach is called naïve. For example, a document that contains the word “insurance” is also likely to contain “beneficiary,” so their presence in messages is not independent.
Nevertheless, even though the independence assumption is usually violated, Naive Bayes classifiers often perform very well. Furthermore, treating properties as independent means that the classifier needs much less data to train than if we had to calculate the conditional probabilities of all combination of properties. Instead, we just have to count separately the number of times each property occurs with each of the two classification outcomes.
-
See (Blanzieri and Bryl 2009) for a review of the spam problem and the policy and technology methods for fighting it. (Upsana and Chakravarty 2010) is somewhat more recent and more narrowly focused on text classification techniques.
A very thorough yet highly readable introduction to Active Learning is (Settles 2012).
-
In particular, documents are usually represented as vectors of frequency-weighted terms. Other approaches start more directly with the similarity measure, obtained either by direct judgments of the similarity of each pair of items or by indirect measures like the accuracy in deciding whether two sounds, colors, or images are the same or different. The assumption is that the confusability of two items reflects how similar they are.
-
Unlike hierarchical clustering methods that have a clear stopping rule when they create the root category, k-means clustering methods run until the centroids of the categorize stabilize. Furthermore, because the k-means algorithm is basically just hill-climbing, and the initial category “seed” items are random, it can easily get stuck in a local optimum. So it is desirable to try many different starting configurations for different choices of K.
-
In addition, the complex feature representations of neural networks compute very precise similarity measurements, which enable searches for specific images or that find duplicate ones.
-
Structure Mapping theory was proposed in (Gentner 1983), and the Structure Mapping Engine followed a few years later (Falkenhainer et al 1989). The SME was criticized for relying on hand-coded knowledge representations, a limitation overcome by (Turney 2008), who used text processing techniques to extract the semantic relationships used by Structure Mapping.

