38 The Semantic Perspective
To describe relationships among resources, we need to understand what the relations mean. This semantic perspective is the essence of relationships and explains why the resources are related, relying on information that is not directly available from perceiving the resources. In our Simpson family example, we noted that Homer and Marge are related by marriage, and also by their relationship as parents of Bart, Lisa, and Maggie, and none of these relationships are directly perceivable. This means that “Homer is married to Marge” is a semantic assertion, but “Homer is standing next to Marge” is not.[1]
Semantic relationships are commonly expressed with a predicate with one or more arguments. A predicate is a verb phrase template for specifying properties of objects or a relationship among objects. In many relationships the predicate is an action or association that involves multiple participants that must be of particular types, and the arguments define the different roles of the participants.[2]
We can express the relationship between Homer and Marge Simpson using a predicate(argument(s)) syntax as follows:
is-married-to (Homer Simpson, Marge Simpson)
The sequence, type, and role of the arguments are an essential part of the relationship expression. The sequence and role are explicitly distinguished when predicates that take two arguments are expressed using a subject-predicate-object syntax that is often called a triple because of its three parts:
Homer Simpson → is-married-to → Marge Simpson
However, we have not yet specified what the “is-married-to” relationship means. People can demonstrate their understanding of “is-married-to” by realizing that alternative and semantically equivalent expressions of the relationship between Homer and Marge might be:
Homer Simpson → is-married-to → Marge Simpson
Homer Simpson → is-the-husband-of → Marge Simpson
Marge Simpson → is-married-to → Homer Simpson
Marge Simpson → is-the-wife-of → Homer Simpson
Going one step further, we could say that people understand the equivalence of these different expressions of the relationship because they have semantic and linguistic knowledge that relates some representation of “married,” “husband,” “wife,” and other words. None of that knowledge is visible in the expressions of the relationships so far, all of which specify concrete relationships about individuals and not abstract relationships between resource classes or concepts. We have simply pushed the problem of what it means to understand the expressions into the mind of the person doing the understanding.
We can be more rigorous and define the words used in these expressions so they are “in the world” rather than just “in the mind” of the person understanding them. We can write definitions about these resource classes:
-
The conventional or traditional marriage relationship is a consensual lifetime association between a husband and a wife, which is sanctioned by law and often by religious ceremonies;
-
A husband is a male lifetime partner considered in relation to his wife; and
-
A wife is a female lifetime partner considered in relation to her husband.[3]
Definitions like these help a person learn and make some sense of the relationship expressions involving Homer and Marge. However, these definitions are not in a form that would enable someone to completely understand the Homer and Marge expressions; they rely on other undefined terms (consensual, law, lifetime, etc.), and they do not state the relationships among the concepts in the definitions.[4] Furthermore, for a computer to understand the expressions, it needs a computer-processable representation of the relationships among words and meanings that makes every important semantic assumption and property precise and explicit. We will see what this takes starting in the next section.
Types of Semantic Relationships
In this discussion we will use entity type, class, concept, and resource type as synonyms. Entity type and class are conventional terms in data modeling and database design, concept is the conventional term in computational or cognitive modeling, and we use resource type when we discuss organizing systems. Similarly, we will use entity occurrence, instance, and resource instance when we refer to one thing rather than to a class or type of them.
There is no real consensus on how to categorize semantic relationships, but these three broad categories are reasonable for our purposes:
- Inclusion Relationship
-
One entity type contains or is comprised of other entity types; often expressed using “is-a,” “is-a-type-of,” “is-part-of,” or “is-in” predicates.
- Attribution Relationship
-
Asserting or assigning values to properties; the predicate depends on the property: “is-the-author-of,” “is-married-to,” “is-employed-by,” etc.
- Possession Relationship
-
Asserting ownership or control of a resource; often expressed using a “has” predicate, such as “has-serial-number-plate.”[5]
All of these are fundamental in organizing systems, both for describing and arranging resources themselves, and for describing the relationships among resources and resource descriptions.
Inclusion
There are three different types of inclusion relationships: class inclusion, meronymic inclusion, and topological inclusion. All three are commonly used in organizing systems.
Class inclusion is the fundamental and familiar “is-a,” “is-a-type-of,” or “subset” relationship between two entity types or classes where one is contained in and thus more specific than the other more generic one.
Meat → is-a → Food
A set of interconnected class inclusion relationships creates a hierarchy, which is often called a taxonomy.
Meat → is-a → Food
Dairy Product → is-a → Food
Cereal → is-a → Food
Vegetable → is-a → Food
Beef → is-a → Meat
Pork → is-a → Meat
Chicken → is-a → Meat
Ground Beef → is-a → Beef
Steak → is-a → Beef
…
A visual depiction of the taxonomy makes the class hierarchy easier to perceive. See Figure: A Partial Taxonomy of Food.
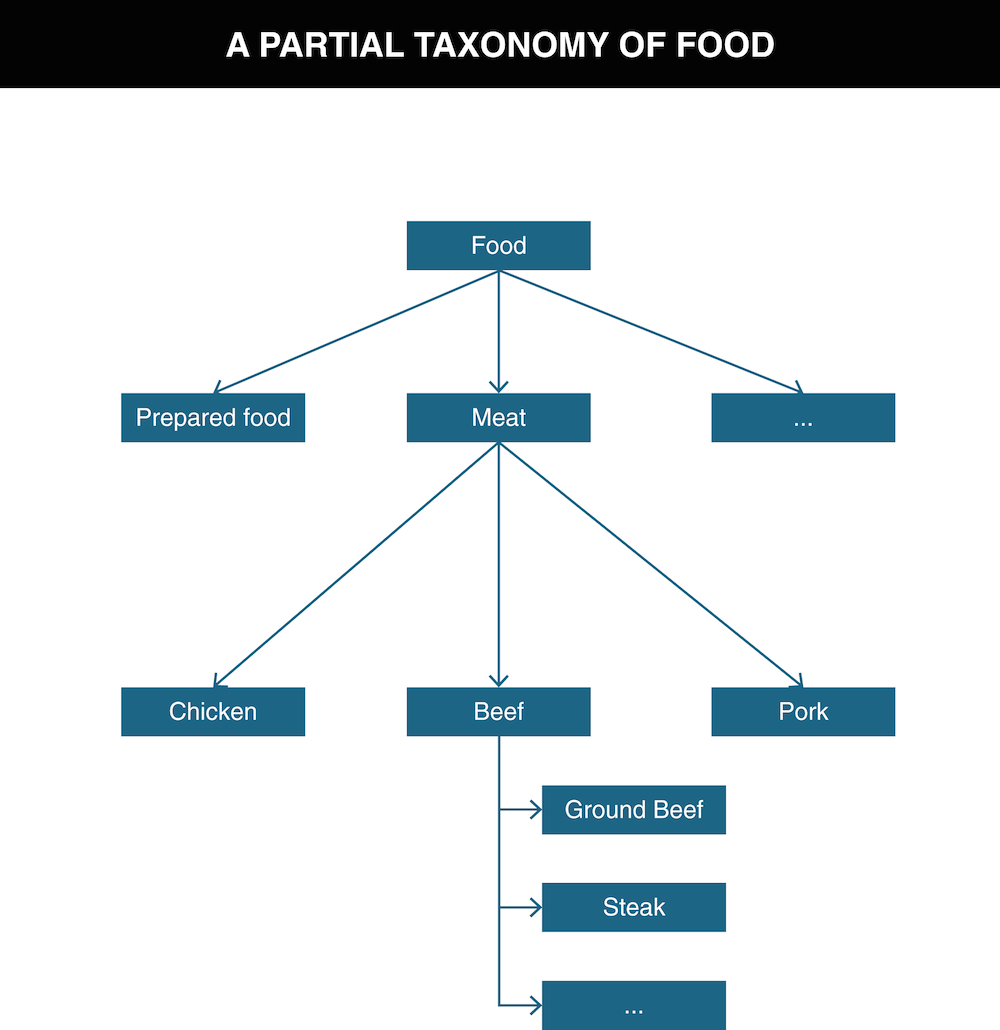
A partial taxonomy of food distinguishes the categories or prepared food from meat, distinguishes chicken, beef, and pork as subcategories of meat, and distinguishes ground beef and steak as subcategories of beef.
Each level in a taxonomy subdivides the class above it into sub-classes, and each sub-class is further subdivided until the differences that remain among the members of each class no longer matter for the interactions the organizing system needs to support. We discuss the design of hierarchical organizing systems in “Principles for Creating Categories”, “Principles for Creating Categories.”
All of the examples in the current section have expressed abstract relationships between classes, in contrast to the earlier concrete ones about Homer and Marge, which expressed relationships between specific people. Homer and Marge are instances of classes like “married people,” “husbands,” and “wives.” When we make an assertion that a particular instance is a member of class, we are classifying the instance. Classification is a class inclusion relationship between an instance and a class, rather than between two classes. (We discuss Classification in detail in Classification: Assigning Resources to Categories.)
Homer Simpson → is-a → Husband
This is just the lowest level of the class hierarchy in which Homer is located at the very bottom; he is also a man, a human being, and a living organism (in cartoon land, at least).[6] You might now remember the bibliographic class inclusion hierarchy we discussed in “Identity and Bibliographic Resources”; a specific physical item like your dog-eared copy of Macbeth is also a particular manifestation in some format or genre, and this expression is one of many for the abstract work.
instance→ is-member-of → class
Part-whole inclusion or meronymic inclusion is a second type of inclusion relationship. It is usually expressed using “is-part-of,” “is-partly,” or with other similar predicate expressions. Winston, Chaffin, and Herrmann identified six distinct types of part-whole relationships. Their meaning subtly differs depending on whether the part is separately identifiable and whether the part is essential to the whole.[7]
-
Component-Object is the relationship type when the part is a separate component that is arranged or assembled with other components to create a larger resource. In “Resources with Parts”, “Resources with Parts,” we used as an example the component-object relationship between an engine and a car:
The Engine → is-part-of → the Car
The components of this type of part-whole relationship need not be physical objects; “Germany is part of the European Union” expresses a component-object relationship. What matters is that the component is identifiable on its own as an integral entity and that the components follow some kind of patterned organization or structure when they form the whole. Together the parts form a composition, and the parts collectively form the whole. A car that lacks the engine part will not work.
-
Member-Collection is the part-whole relationship type where “is-part-of” means “belongs-to,” a weaker kind of association than component-object because there is no assumption that the component has a specific role or function in the whole.
The Book → is-part-of → the Library
The members of the collection exist independently of the whole; if the whole ceases to exist the individual resources still exist.
-
Portion-Mass is the relationship type when all the parts are similar to each other and to the whole, unlike either of the previous types where engines are not tires or cars, and books are not like record albums or libraries.
The Slice → is-part-of → the Pie
-
Stuff-Object relationships are most often expressed using “is-partly” or “is-made-of” and are distinguishable from component-object ones because the stuff cannot be separated from the object without altering its identity. The stuff is not a separate ingredient that is used to make the object; it is a constituent of it once it is made.
Wine → is-partly → Alcohol
-
Place-Area relationships exist between areas and specific places or locations within them. Like members of collections, places have no particular functional contribution to the whole.
The Everglades → are-part-of → Florida
-
Feature-Activity is a relationship type in which the components are stages, phases, or sub activities that take place over time. This relationship is similar to component-object in that the components in the whole are arranged according to a structure or pattern.
Overtime → is-part-of → a Football Game
A seventh type of part-whole relationship called Phase-Activity was proposed by Storey.[8]
-
Phase-Activity is similar to feature-activity except that the phases do not make sense as standalone activities without the context provided by the activity as a whole.
Paying → is-part-of → Shopping
Topological, Locative and Temporal Inclusion is a third type of inclusion relationship between a container, area, or temporal duration and what it surrounds or contains. It is most often expressed using “is-in” as the relationship. However, the entity that is contained or surrounded is not a part of the including one, so this is not a part-whole relationship.
The Vatican City → is-in → Italy
The meeting → is-in → the afternoon
Attribution
In contrast to inclusion expressions that state relationships between resources, attribution relationships assert or assign values to properties for a particular resource. In Resource Description and Metadata we used “attribute” to mean “an indivisible part of a resource description” and treated it as a synonym of “property.” We now need to be more precise and carefully distinguish between the type of the attribute and the value that it has. For example, the color of any object is an attribute of the object, and the value of that attribute might be “green.”
Some frameworks for semantic modeling define “attribute” very narrowly, restricting it to expressions with predicates with only one argument to assert properties of a single resource, distinguishing them from relationships between resources or resource types that require two arguments:[9]
Martin the Gecko → is-small
Martin the Gecko → is-green
However, it is always possible to express statements like these in ways that make them into relationships with two arguments:
Martin → has-size → small
Martin → has-skin-color → green
Dedre Gentner notes that this supposed distinction between one-predicate attributes and two-predicate relationships depends on context.[10]
For example, small can be viewed as an attribute, X → is-small, or as a relationship between X and some standard or reference Y, X → is-smaller-than → Y.
Another somewhat tricky aspect of attribution relationships is that from a semantic perspective, there are often many different ways of expressing equivalent attribute values.
Martin → has-size → 6 inches
Martin → has size → 152 mm
These two statements express the idea that Martin is small. However, many implementations of attribution relationships treat the attribute values literally. This means that unless we can process these two statements using another relationship that expresses the conversion of inches to mm, the two statements could be interpreted as saying different things about Martin’s size.
Finally, we note that we can express attribution relationships about other relationships, like the date a relationship was established. Homer and Marge Simpson’s wedding anniversary is an attribute of their “is-married-to” relationship.
The semantic distinctions between attributes and other types of relationships are not strong ones, but they can be made clearer by implementation choices. For example, XML attributes are tightly coupled to a containing element, and their literal values are limited to atomic items of information. In contrast, inclusion relationships are expressed by literal containment of one XML element by another.
Possession
A third distinct category of semantic relationships is that of possession. Possession relationships can seem superficially like part-whole ones:
Bob → has → a car
A car → has → wheels
However, in the second of these relationships “has” is an elliptical form of “has as a part,” expressing a part-whole relationship rather that one of possession.
The concept of possession is especially important in institutional organizing systems, where questions of ownership, control, responsibility and transfers of ownership, control, and responsibility can be fundamental parts of the interactions they support. However, possession is a complex notion, inherently connected to societal norms and conventions about property and kinship, making it messier than institutional processes might like.
Possession relationships also imply duration or persistence, and are often difficult to distinguish from relationships based on habitual location or practice. Miller and Johnson-Laird illustrate the complex nature of possession relationships with this sentence, which expresses three different types of them:[11]
-
He owns an umbrella but she’s borrowed it, though she doesn’t have it with her.
Properties of Semantic Relationships
Semantic relationships can have numerous special properties that help explain what they mean and especially how they relate to each other. In the following sections we briefly explain those that are most important in systems for organizing resources and resource descriptions.
Symmetry
In most relationships the order in which the subject and object arguments are expressed is central to the meaning of the relationship. If X has a relationship with Y, it is usually not the case that Y has the same relationship with X. For example, because “is-parent-of” is an asymmetric relationship, only the first of these relationships holds:
Homer Simpson → is-parent-of → Bart Simpson (TRUE)
Bart Simpson → is-parent-of → Homer Simpson (NOT TRUE)
In contrast, some relationships are symmetric or bi-directional, and reversing the order of the arguments of the relationship predicate does not change the meaning. As we noted earlier, these two statements are semantically equivalent because “is-married-to” is symmetric:
Homer Simpson → is-married-to → Marge Simpson
Marge Simpson → is-married-to → Homer Simpson
We can represent the symmetric and bi-directional nature of these relationships by using a double-headed arrow:
Homer Simpson ⇔ is-married-to ⇔ Marge Simpson
Transitivity
Transitivity is another property that can apply to semantic relationships. When a relationship is transitive, if X and Y have a relationship, and Y and Z have the same relationship, then X also has the relationship with Z. Any relationship based on ordering is transitive, which includes numerical, alphabetic, and chronological ones as well as those that imply qualitative or quantitative measurement. Because “is-taller-than” is transitive:
Homer Simpson → is-taller-than → Bart Simpson
Bart Simpson → is-taller-than → Maggie Simpson
implies that:
Homer Simpson → is-taller-than → Maggie Simpson
Inclusion relationships are inherently transitive, because just as “is-taller-than” is an assertion about relative physical size, “is-a-type of” and “is-part-of” are assertions about the relative sizes of abstract classes or categories. An example of transitivity in part-whole or meronymic relationships is: (1) the carburetor is part of the engine, (2) the engine is part of the car, (3) therefore, the carburetor is part of the car. [12]
Transitive relationships enable inferences about class membership or properties, and allow organizing systems to be more efficient in how they represent them since transitivity enables implicit relationships to be made explicit only when they are needed.
Equivalence
Any relationship that is both symmetric and transitive is an equivalence relationship; “is-equal-to” is obviously an equivalence relationship because if A=B then B=A and if A=B and B=C, then A=C. Other relationships can be equivalent without meaning “exactly equal,” as is the relationship of “is-congruent-to” for all triangles.
We often need to assert that a particular class or property has the same meaning as another class or property or that it is generally substitutable for it. We make this explicit with an equivalence relationship.
Sister (English) ⇔ is-equivalent-to ⇔ Hermana (Spanish)
Inverse
For asymmetric relationships, it is often useful to be explicit about the meaning of the relationship when the order of the arguments in the relationship is reversed. The resulting relationship is called the inverse or the converse of the first relationship. If an organizing system explicitly represents that:
We can then conclude that:
Bart Simpson → is-child-of → Homer Simpson
Ontologies
We now have described types and properties of semantic relationships in enough detail to return to the challenge we posed earlier: what information is required to fully understand relationships? This question has been asked and debated for decades and we will not pretend to answer it to any extent here. However, we can sketch out some of the basic parts of the solution.
Let us begin by recalling that a taxonomy captures a system of class inclusion relationships in some domain. But as we have seen, there are a great many kinds of relationships that are not about class inclusion. All of these other types of relationships represent knowledge about the domain that is potentially needed to understand statements about it and to make sense when more than one domain of resources or activities comes together.
For example, in the food domain whose partial taxonomy appears in Figure: A Partial Ontology of Food., we can assert relationships about properties of classes and instances, express equivalences about them, and otherwise enhance the representation of the food domain to create a complex network of relationships. In addition, the food domain intersects with food preparation, agriculture, commerce, and many other domains. We also need to express the relationships among these domains to fully understand any of them.
Grilling → is-a-type-of → Food Preparation
Temperature → is-a-measure-of → Grilling
Hamburger → is-equivalent-to → Ground Beef
Hamburger → is-prepared-by → Grilling
Hamburger Sandwich → is-a-type-of → Prepared Food
Rare → is-a → State of Food Preparation
Well-done → is-a → State of Food Preparation
Meat → is-preserved-by → Freezing
Thawing → is-the-inverse-of → Freezing
…
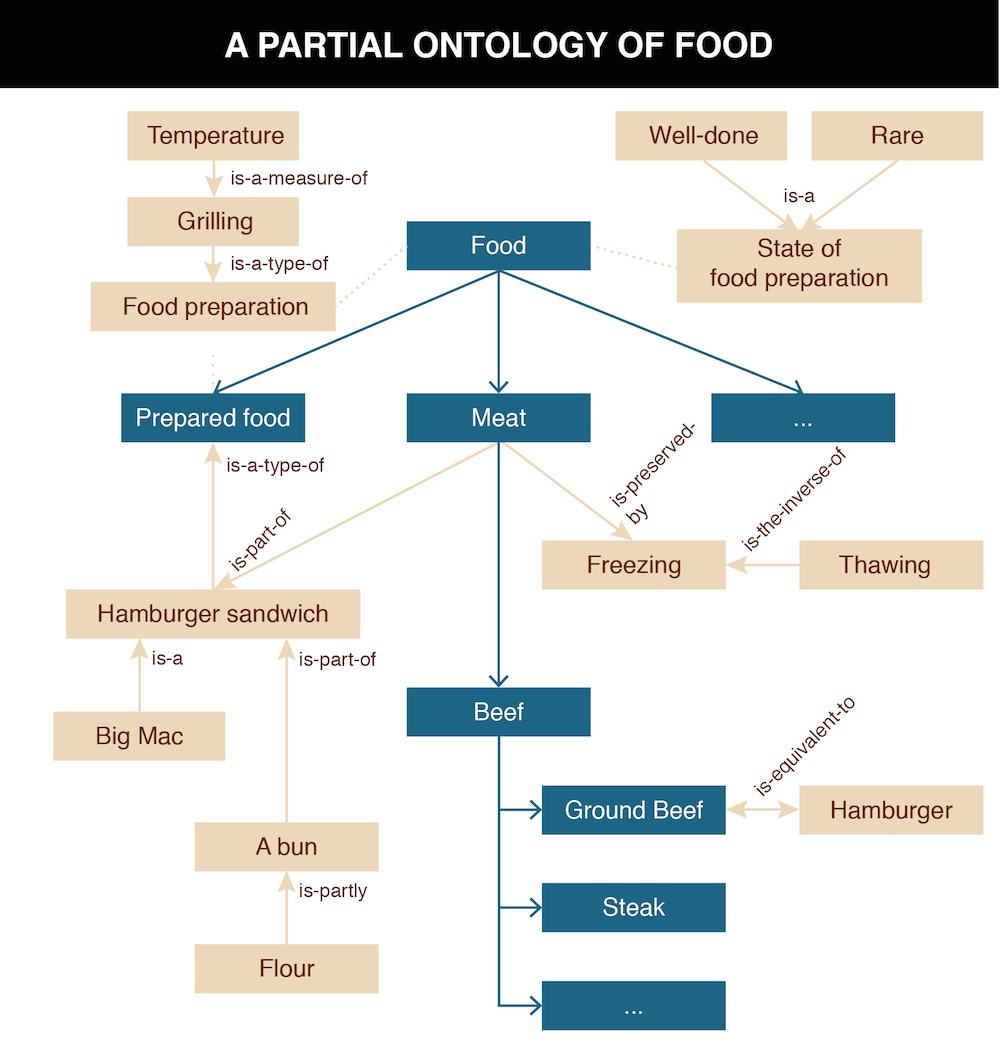
A partial ontology of food overlays the taxonomy of food with statements that make assertions about categories, instances, and relationships in the food domain. Example statements might be that “Grilling is a type of food preparation,” that “Meat is preserved by freezing,” and that “Hamburger is equivalent to ground beef.”
In this simple example we see that class inclusion relationships form a kind of backbone to which other kinds of relationships attach. We also see that there are many potentially relevant assertions that together represent the knowledge that just about everyone knows about food and related domains. A network of relationships like these creates a resource that is called an ontology.[13] A visual depiction of the ontology illustrates this idea that it has a taxonomy as its conceptual scaffold. (See Figure: A Partial Ontology of Food.)
There are numerous formats for expressing ontologies, but many of them have recently converged to or are based on the Web Ontology Language(OWL), developed by the W3C. OWL ontologies use a formal logic-based language that builds on RDF (“Resource Description Framework (RDF)”) to define resource classes and assign properties to them in rigorous ways, arrange them in a class hierarchy, establish their equivalence, and specify the properties of relationships.[14]
Ontologies are essential parts in some organizing systems, especially information-intensive ones where the scope and scale of the resources require an extensive and controlled description vocabulary. (See “The Process of Describing Resources”.) The most extensive ontology ever created is Cyc, born in 1984 as an artificial intelligence research project. Three decades later, the latest version of the Cyc ontology contains several hundred thousand terms and millions of assertions that interrelate them.[15]
-
“Semantic” is usually defined as “relating to meaning or language” and that does not seem helpful here.
-
For decades important and vexing questions have been raised about the specificity of these predicate-argument associations and how or when the semantic constraints they embody combine with syntactic and contextual constraints during the process of comprehending language. Consider how “While in the operating room, the surgeon used a knife to cut the ____” generates a different expectancy from the same predicate and agent in “While at the fancy restaurant, the surgeon used a knife to cut the ____.” See (Elman 2009).
-
This book is not the place for the debate over the definition of marriage. We are not bigots; we just do not need this discussion here. If these definitions upset you here, you will feel better in “Degree”.
-
Typically, when people use language they operate on the assumption that everyone shares their model of the world, providing the common ground that enables them to communicate. As we saw in Resources in Organizing Systems and Resource Description and Metadata, (because of the vocabulary problem and different purposes for using resources and language) this assumption is often wrong, This paves the way for serious misunderstandings, since what is assumed to be shared knowledge may not really be shared or understood the same way.
-
Which of these classifications is most relevant depends on the context. In addition, there might be other Homer Simpsons who are not cartoon characters or who are not married, so we might have to disambiguate this homonymy to make sure we referring to the intended Homer Simpson.
-
Martin is the animated gecko who is the advertising spokesman for Geico Insurance (
http://www.geico.com/). Martin’s wit and cockney accent make him engaging and memorable, and a few years ago he was voted the favorite advertising icon in the US. -
Some people have argued that meronomy is not transitive, but a closer look at their supposed counter-examples suggests otherwise. See Section 5 in (Winston, Chaffin, and Herman 1987).
-
ontology is a branch of philosophy concerned with what exists in reality and the general features and relations of whatever that might be (Hofweber 2009). Computer science has adopted “ontology” to refer to any computer-processable resource that represents the relationships among words and meanings in some knowledge domain. See (Gruber 1993), (Guarino 1998).
-
Web Ontology Language(OWL)
http://www.w3.org/2004/OWL/.

